Kotlin Functors, Applicatives, And Monads In Picture

This is a translation of Functors, Applicatives, And Monads In Pictures from Haskell into Kotlin. I have also translated this into Chinese: Kotlin 版图解 Functor、Applicative 与 Monad.

Different from the Kotlin translation from Swift, this is translated directly from the original article.

If you enjoy this post be sure to say thanks to the author of the original version: Aditya Bhargava, @_egonschiele on Twitter.

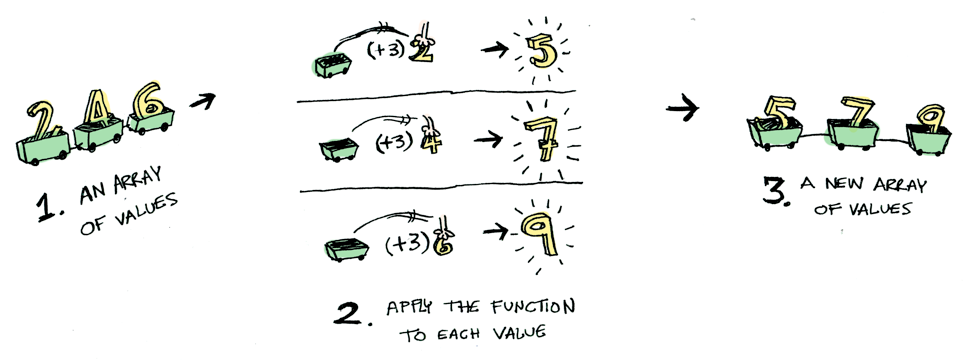
Here’s a simple value:

And we know how to apply a function to this value:

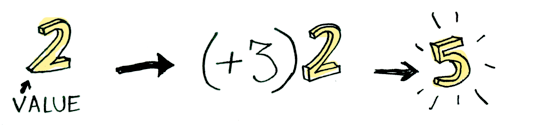
Simple enough. Lets extend this by saying that any value can be in a context. For now you can think of a context as a box that you can put a value in:

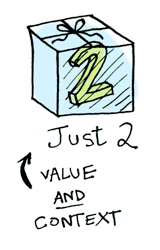
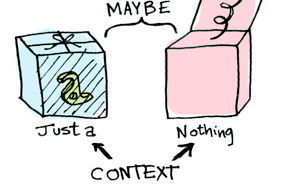
Now when you apply a function to this value, you’ll get different results depending on the context. This is the idea that Functors, Applicatives, Monads, Arrows etc are all based on. The Maybe data type defines two related contexts:

sealed class Maybe<out T> {
    object `Nothing#` : Maybe<Nothing>() {
        override fun toString(): String = "Nothing#"
    }
    data class Just<out T>(val value: T) : Maybe<T>()
}

In a second we’ll see how function application is different when something is a Just<T> versus a Nothing#. First let’s talk about Functors!

Note: Here use Nothing# instead of Nothing, since Nothing is a special type in Kotlin, see The Nothing type. And Kotlin has its own way for representing optinal value instead of using Maybe-like type, see Null Safety.

Functors

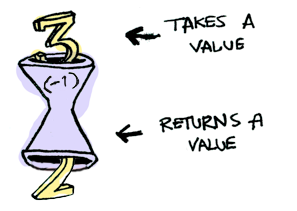
When a value is wrapped in a context, you can’t apply a normal function to it:

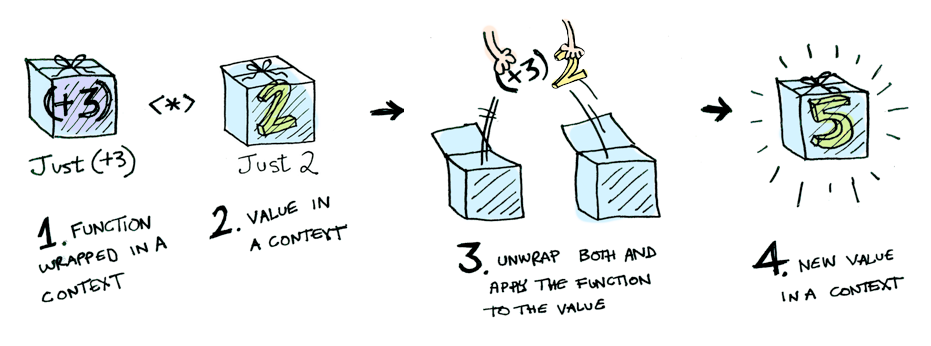
This is where fmap comes in. fmap is from the street, fmap is hip to contexts. fmap knows how to apply functions to values that are wrapped in a context. For example, suppose you want to apply { it + 3 } to Just(2). Use fmap:

> Maybe.Just(2).fmap { it + 3 }
Just(value=5)

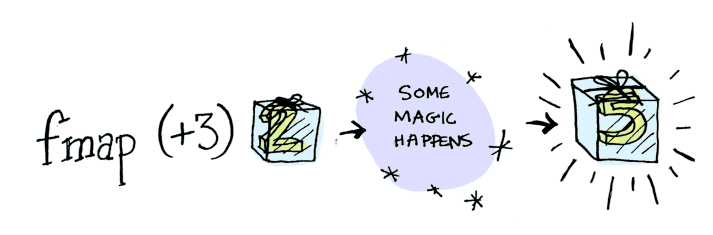
Bam! fmap shows us how it’s done! But how does fmap know how to apply the function?

Just what is a Functor, really?

Functor is a typeclass in Haskell. Here’s the definition:

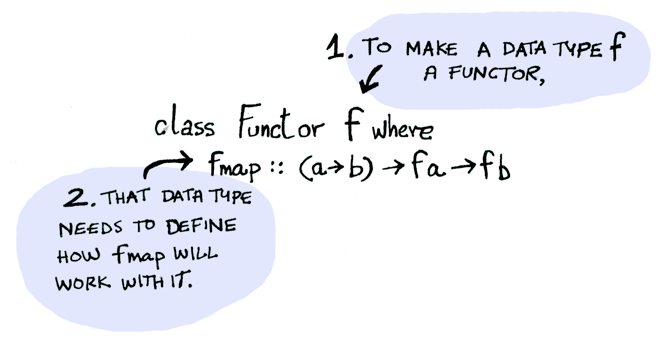
In Kotlin, Functor can be considered as a type that defines fmap method/extension function. Here’s how fmap works:

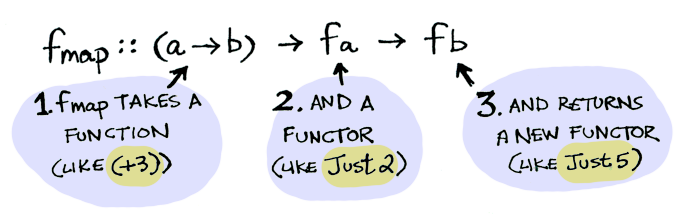
So we can do this:

> Maybe.Just(2).fmap { it + 3 }
Just(value=5)

And fmap magically applies this function, because Maybe is a Functor. It specifies how fmap applies to Justs and Nothing#s:

fun <T, R> Maybe<T>.fmap(transform: (T) -> R): Maybe<R> = when(this) {
    Maybe.`Nothing#` -> Maybe.`Nothing#`
    is Maybe.Just -> Maybe.Just(transform(this.value))
}

Here’s what is happening behind the scenes when we write Maybe.Just(2).fmap { it + 3 }:

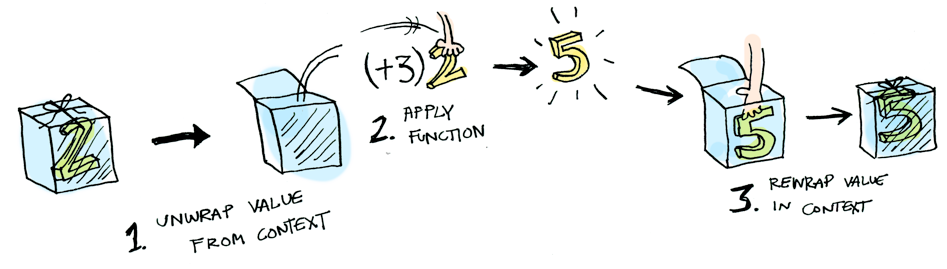
So then you’re like, alright fmap, please apply { it + 3 } to a Nothing#?

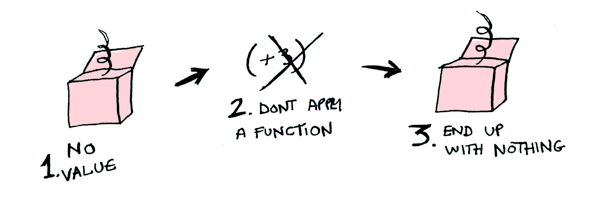
> Maybe.`Nothing#`.fmap { x: Int -> x + 3 }
Nothing#

Note: Here the argument type of the lambda must be annotated explicitly, since there are many types can plus an Int in Kotlin.

Bill O'Reilly being totally ignorant about the Maybe functor

Like Morpheus in the Matrix, fmap knows just what to do; you start with Nothing#, and you end up with Nothing#! fmap is zen. Now it makes sense why the Maybe data type exists. For example, here’s how you work with a database record in a language without Maybe:

post = Post.find_by_id(1)
if post
    return post.title
else
    return nil
end

But in Kotlin:

findPost(1).fmap(::getPostTitle)

If findPost returns a post, we will get the title with getPostTitle. If it returns Nothing#, we will return Nothing#! Pretty neat, huh?

We can even define an infix operator for fmap, ($) (<$> in Haskell), and you will often see this instead:

infix fun <T, R> ((T) -> R).`($)`(maybe: Maybe<T>) = maybe.fmap(this)

::getPostTitle `($)` findPost(1)

Here’s another example: what happens when you apply a function to an Iterable(List in Haskell)?

Iterables are functors too! We can define the fmap for them:

fun <T, R> Iterable<T>.fmap(transform: (T) -> R): List<R> = this.map(transform)

Okay, okay, one last example: what happens when you apply a function to another function?

{ x: Int - > x + 1 }.fmap { x: Int -> x + 3 }

Here’s a function:

Here’s a function applied to another function:

The result is just another function!

> fun <T, U, R> ((T) -> U).fmap(transform: (U) -> R) = { t: T -> transform(this(t)) }
> val foo = { x: Int -> x + 2 }.fmap { x: Int -> x + 3 }
> foo(10)
15

So functions are Functors too! When you use fmap on a function, you’re just doing function composition!

Applicatives

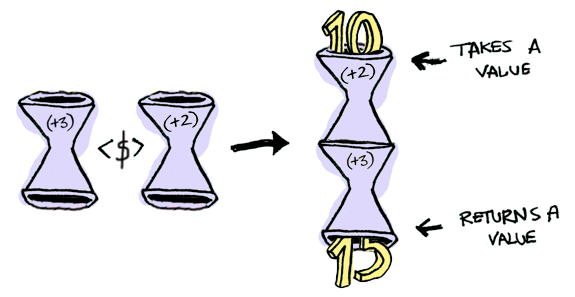
Applicatives take it to the next level. With an applicative, our values are wrapped in a context, just like Functors:

But our functions are wrapped in a context too!

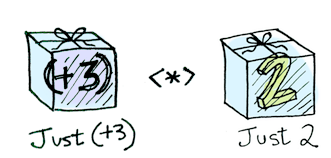
Yeah. Let that sink in. Applicatives don’t kid around. Applicative defines (*) (<*> in Haskell), which knows how to apply a function wrapped in a context to a value wrapped in a context:

i.e:

infix fun <T, R>  Maybe<(T) -> R>.`(*)`(maybe: Maybe<T>): Maybe<R> = when(this) {
    Maybe.`Nothing#` -> Maybe.`Nothing#`
    is Maybe.Just -> this.value `($)` maybe
}

Maybe.Just { x: Int -> x + 3 } `(*)` Maybe.Just(2) == Maybe.Just(5)

Using (*) can lead to some interesting situations. For example:

infix fun <T, R>  Iterable<(T) -> R>.`(*)`(iterable: Iterable<T>) = this.flatMap { iterable.map(it) }

With this definition, we can apply a list of functions to a list of values:

> listOf<(Int) -> Int>({ it * 2 }, { it + 3 }) `(*)` listOf(1, 2, 3)
[2, 4, 6, 4, 5, 6]

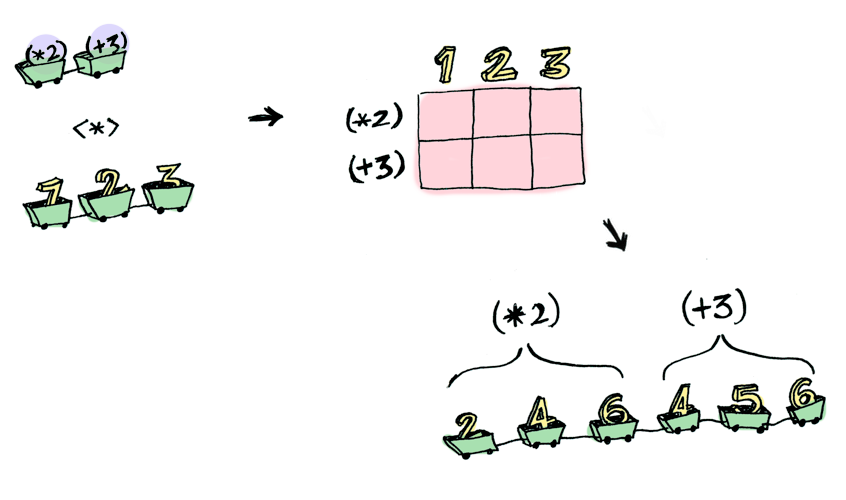
Here’s something you can do with Applicatives that you can’t do with Functors. How do you apply a function that takes two arguments to two wrapped values?

> { y: Int -> { x: Int -> x + y } } `($)` Maybe.Just(5)
Just(value=(kotlin.Int) -> kotlin.Int) // equal to `Maybe.Just { x: Int -> x + 5 }`
> Maybe.Just { x: Int -> x + 5 } `($)` Maybe.Just(4)
ERROR ??? WHAT DOES THIS EVEN MEAN WHY IS THE FUNCTION WRAPPED IN A JUST

Applicatives:

> { y: Int -> { x: Int -> x + y } } `($)` Maybe.Just(5)
Just(value=(kotlin.Int) -> kotlin.Int) // equal to `Maybe.Just { x: Int -> x + 5 }`
> Maybe.Just { x: Int -> x + 5 } `(*)` Maybe.Just(3)
Just(value=8)

Applicative pushes Functor aside. “Big boys can use functions with any number of arguments,” it says. “Armed ($) and (*), I can take any function that expects any number of unwrapped values. Then I pass it all wrapped values, and I get a wrapped value out! AHAHAHAHAH!”

> { y: Int -> { x: Int -> x + y } } `($)` Maybe.Just(5) `(*)` Maybe.Just(3)
Just(value=15)

We can also define another Applicative’s function liftA2:

fun <T> ((x: T, y: T) -> T).liftA2(m1: Maybe<T>, m2: Maybe<T>) =
    { y: T -> { x: T -> this(x, y) } } `($)` m1 `(*)` m2

And using liftA2 do the same thing:

> { x: Int, y: Int -> x * y }.liftA2(Maybe.Just(5), Maybe.Just(3))
Just(value=15)

Monads

How to learn about Monads:

Get a PhD in computer science.
Throw it away because you don’t need it for this section!

Monads add a new twist.

Functors apply a function to a wrapped value:

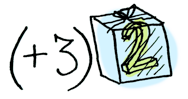
Applicatives apply a wrapped function to a wrapped value:

Monads apply a function that returns a wrapped value to a wrapped value. Monads have a function ))= (>>= in Haskell, pronounced “bind”) to do this.

Let’s see an example. Good ol’ Maybe is a monad:

Just a monad hanging out

Suppose half is a function that only works on even numbers:

fun half(x: Int) = if (x % 2 == 0)
                       Maybe.Just(x / 2)
                   else
                       Maybe.`Nothing#`

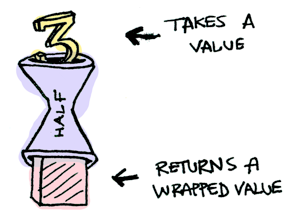
What if we feed it a wrapped value?

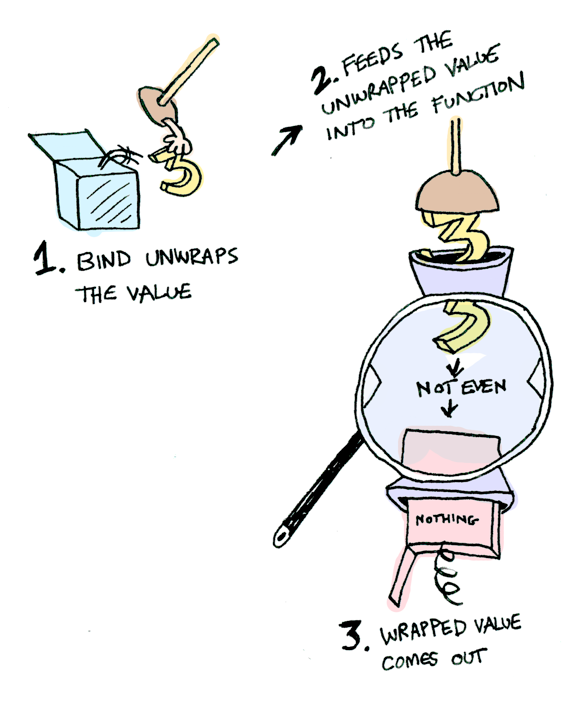
We need to use ))= to shove our wrapped value into the function. Here’s a photo of ))=:

Here’s how it works:

> Maybe.Just(3) `))=` ::half
Nothing#
> Maybe.Just(4) `))=` ::half
Just(value=2)
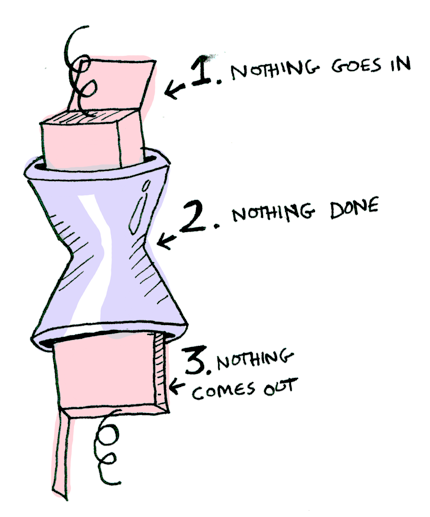
> Maybe.`Nothing#` `))=` ::half
Nothing#

What’s happening inside? Monad is another typeclass in Haskell. Here’s a partial definition (in Haskell):

class Monad m where
    (>>=) :: m a -> (a -> m b) -> m b

Where >>= is:

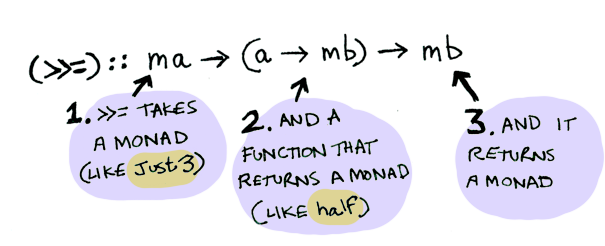
In Kotlin, Monad can be considered as a type that defines such an infix function:

infix fun <T, R> Monad<T>.`))=`(f: ((T) -> Monad<R>)): Monad<R>

So Maybe is a Monad:

infix fun <T, R> Maybe<T>.`))=`(f: ((T) -> Maybe<R>)): Maybe<R> = when(this) {
    Maybe.`Nothing#` -> Maybe.`Nothing#`
    is Maybe.Just -> f(this.value)
}

Here it is in action with a Just(3)!

And if you pass in a Nothing# it’s even simpler:

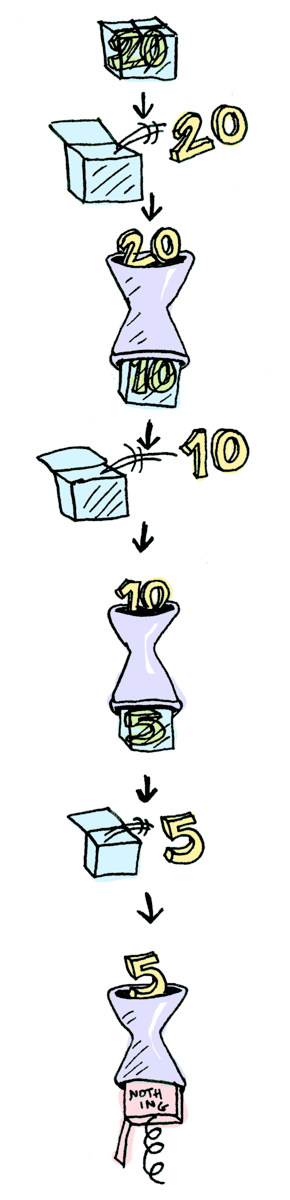
You can also chain these calls:

> Maybe.Just(20) `))=` ::half `))=` ::half `))=` ::half
Nothing#

Note: The built-in null safety syntax of Kotlin can provide monad-like operations including chaining the calls:
fun Int.half() = if (this % 2 == 0) this / 2 else null

val n: Int? = 20
n?.half()?.half()?.half()

Cool stuff! So now we know that Maybe is a Functor, an Applicative, and a Monad.

Now let’s mosey on over to another example: the IO monad:

Note: Since Kotlin doesn’t distinguish between pure and impure function, it doesn’t need IO monad at all. This is just an emulation:
data class IO<out T>(val `(-`: T)

infix fun <T, R> IO<T>.`))=`(f: ((T) -> IO<R>)): IO<R> = f(this.`(-`)

Specifically three functions. getLine takes no arguments and gets user input:

fun getLine(): IO<String> = IO(readLine() ?: "")

readFile takes a string (a filename) and returns that file’s contents:

typealias FilePath = String

fun readFile(filename: FilePath): IO<String> = IO(File(filename).readText())

putStrLn takes a string and prints it:

fun putStrLn(str: String): IO<Unit> = IO(println(str))

All three functions take a regular value (or no value) and return a wrapped value. We can chain all of these using ))=!

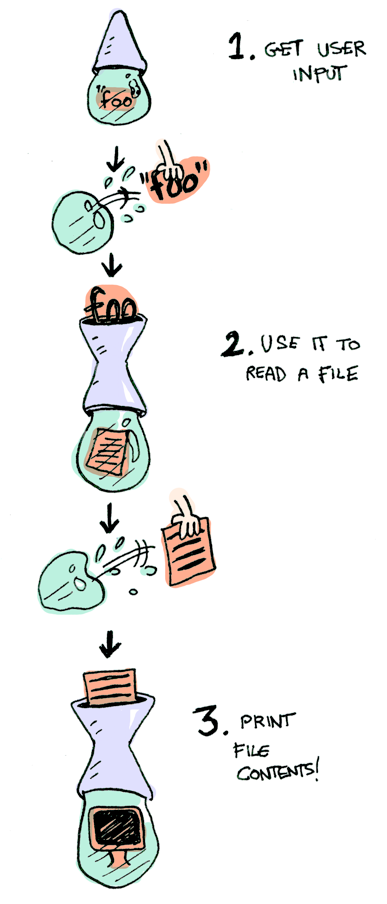
getLine() `))=` ::readFile `))=` ::putStrLn

Aw yeah! Front row seats to the monad show! Haskell also provides us with some syntactical sugar for monads, called do notation:

foo = do
    filename <- getLine
    contents <- readFile filename
    putStrLn contents

It can be emulated in Kotlin (where the <- operator in haskell is replaced with (- property and assignment):

fun <T> `do` (ioOperations: () -> IO<T>) = ioOperations()

val foo = `do` {
  val filename = getLine().`(-`
  val contents = readFile(filename).`(-`
  putStrLn(contents)
}

Conclusion

A functor (in haskell) is a data type that implements the Functor typeclass.
An applicative (in haskell) is a data type that implements the Applicative typeclass.
A monad (in haskell) is a data type that implements the Monad typeclass.
A Maybe implements all three, so it is a functor, an applicative, and a monad.

What is the difference between the three?

functors: you apply a function to a wrapped value using fmap or ($)
applicatives: you apply a wrapped function to a wrapped value using (*) or liftA
monads: you apply a function that returns a wrapped value, to a wrapped value using ))= or liftM

So, dear friend (I think we are friends by this point), I think we both agree that monads are easy and a SMART IDEA(tm). Now that you’ve wet your whistle on this guide, why not pull a Mel Gibson and grab the whole bottle. Check out LYAH’s section on Monads. There’s a lot of things I’ve glossed over because Miran does a great job going in-depth with this stuff.

Follow me on Twitter: JiaYanwei(hltj).